Сумма внешних углов многоугольника - важная геометрическая характеристика, которая имеет постоянное значение для любых выпуклых многоугольников. Рассмотрим это свойство подробнее.
Содержание
Определение внешнего угла
Внешний угол многоугольника - это угол, смежный с внутренним углом фигуры. Он образуется продолжением одной из сторон многоугольника.
- Внешний угол дополняет внутренний до 180°
- Для каждой вершины можно построить два внешних угла
- Обычно рассматривают внешние углы, направленные "наружу" многоугольника
Теорема о сумме внешних углов
Для любого выпуклого n-угольника сумма внешних углов, взятых по одному при каждой вершине, равна 360°.
| Тип многоугольника | Количество сторон | Сумма внешних углов |
| Треугольник | 3 | 360° |
| Четырехугольник | 4 | 360° |
| Пятиугольник | 5 | 360° |
| n-угольник | n | 360° |
Доказательство теоремы
- В каждой вершине сумма внутреннего и внешнего углов равна 180°
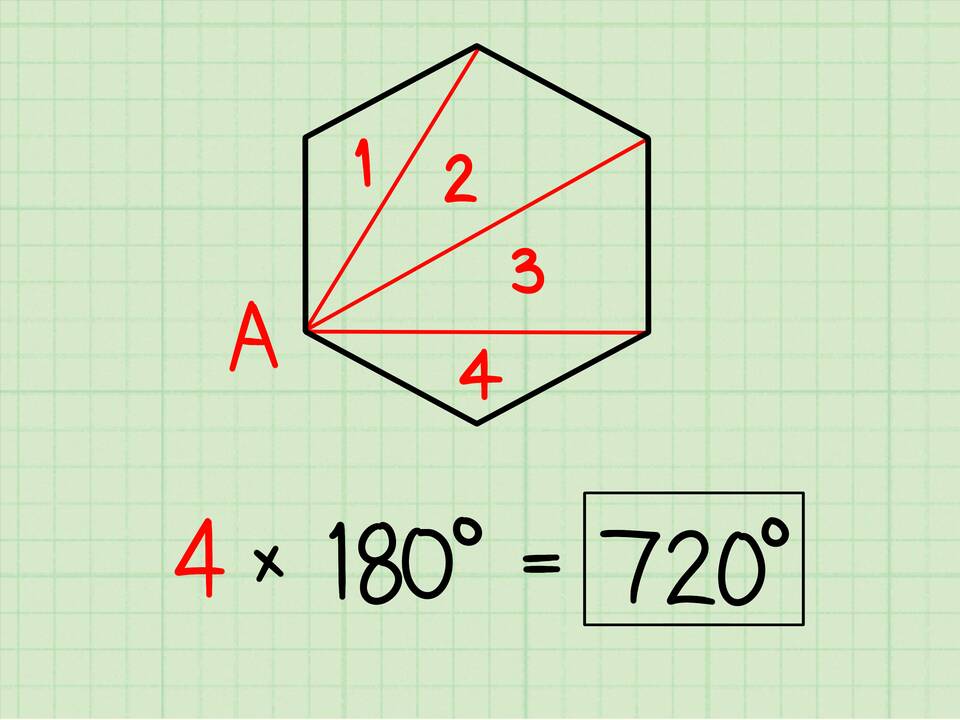
- Сумма внутренних углов n-угольника равна (n-2)×180°
- Общая сумма всех углов (внутренних и внешних) равна n×180°
- Вычитая сумму внутренних углов, получаем сумму внешних: n×180° - (n-2)×180° = 360°
Пример расчета
Для правильного пятиугольника:
- Внутренний угол = 108°
- Внешний угол = 180° - 108° = 72°
- Сумма 5 внешних углов = 5×72° = 360°
Важные замечания
Теорема справедлива только для выпуклых многоугольников. Для невыпуклых многоугольников сумма внешних углов может отличаться от 360°, но при правильном учете направлений углов (с учетом знаков) алгебраическая сумма также будет равна 360°.