Вычисление суммы длин всех ребер геометрической фигуры - важная задача в геометрии, применяемая в различных инженерных и архитектурных расчетах. Рассмотрим методы расчета для разных типов фигур.
Содержание
Вычисление суммы длин всех ребер геометрической фигуры - важная задача в геометрии, применяемая в различных инженерных и архитектурных расчетах. Рассмотрим методы расчета для разных типов фигур.
Основные принципы расчета
| Тип фигуры | Количество ребер | Особенности расчета |
| Многогранники | Зависит от типа фигуры | Сумма длин всех сторон |
| Призмы | 3n (n-угольная призма) | 2 основания + боковые ребра |
| Пирамиды | 2n (n-угольная пирамида) | Основание + боковые ребра |
Пошаговый алгоритм расчета
1. Определение типа фигуры
- Установите, является ли фигура правильной
- Определите количество граней и ребер
- Выясните, все ли ребра равны по длине
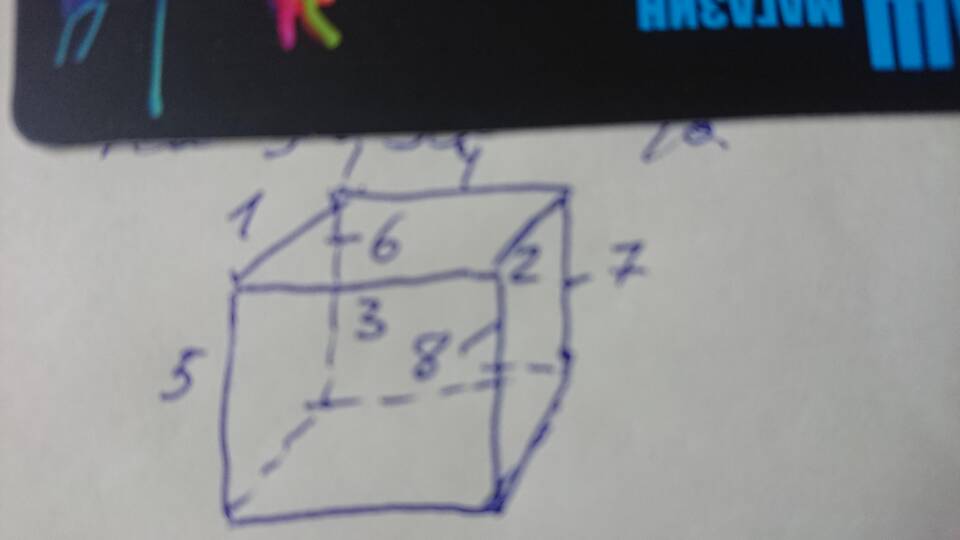
2. Расчет для куба
- Количество ребер: 12
- Формула: L = 12a
- Где a - длина одного ребра
3. Расчет для прямоугольного параллелепипеда
| Тип ребер | Количество | Формула частичной суммы |
| Длина (a) | 4 | 4a |
| Ширина (b) | 4 | 4b |
| Высота (c) | 4 | 4c |
| Общая сумма | 12 | 4(a + b + c) |
Примеры расчетов
Правильная четырехугольная пирамида
- Основание: 4 ребра по a см
- Боковые ребра: 4 ребра по b см
- Общая сумма: L = 4a + 4b = 4(a + b)
Треугольная призма
- Основания: 2 × 3 ребра по a см
- Боковые ребра: 3 ребра по h см
- Общая сумма: L = 6a + 3h = 3(2a + h)
Практическое применение
Знание суммы длин ребер необходимо при расчете материалов для каркасов, определении длины сварных швов или декоративных элементов. Для сложных фигур рекомендуется составлять таблицу всех ребер с указанием их длин перед суммированием.
